Next Permutation

A permutation of an array of integers is an arrangement of its members into a sequence or linear order.

• For example, for arr = [1,2,3], the following are considered permutations of arr: [1,2,3], [1,3,2], [3,1,2], [2,3,1].

The next permutation of an array of integers is the next lexicographically greater permutation of its integer. More formally, if all the permutations of the array are sorted in one container according to their lexicographical order, then the next permutation of that array is the permutation that follows it in the sorted container. If such arrangement is not possible, the array must be rearranged as the lowest possible order (i.e., sorted in ascending order).

• For example, the next permutation of arr = [1,2,3] is [1,3,2].
• Similarly, the next permutation of arr = [2,3,1] is [3,1,2].
• While the next permutation of arr = [3,2,1] is [1,2,3] because [3,2,1] does not have a lexicographical larger rearrangement. Given an array of integers nums, find the next permutation of nums.

The replacement must be in place and use only constant extra memory.

How to Solve

First, we observe that for any given sequence that is in descending order, no next larger permutation is possible. For example, no next permutation is possible for the array: [9, 5, 4, 3, 1].

We need to find the first pair of two successive numbers a[i] and a[i−1], from the right, which satisfy a[i] > a[i-1].

Now, no rearrangements to the right of a[i-1] can create a larger permutation since that subarray consists of numbers in descending order. Thus, we need to rearrange the numbers to the right of a[i−1] including itself.

Now, what kind of rearrangement will produce the next larger number?

We want to create the permutation just larger than the current one. Therefore, we need to replace the number a[i-1] with the number which is just larger than itself among the numbers lying to its right section, say a[j].

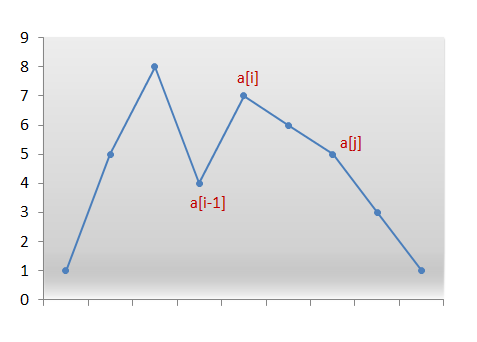
We swap the numbers a[i-1] and a[j]. We now have the correct number at index i-1. But still the current permutation isn’t the permutation that we are looking for. We need the smallest permutation that can be formed by using the numbers only to the right of a[i-1]. Therefore, we need to place those numbers in ascending order to get their smallest permutation.

But, recall that while scanning the numbers from the right, we simply kept decrementing the index until we found the pair a[i] and a[i-1] where, a[i] > a[i-1]. Thus, all numbers to the right of a[i−1] were already sorted in descending order. Furthermore, swapping a[i-1] and a[j] didn’t change that order. Therefore, we simply need to reverse the numbers following a[i-1] to get the next smallest lexicographic permutation.

Test Cases

Input:

  (int[]) nums = [1,2,3]

Output:

  (int[]) [1,3,2]

Input:

  (int[]) nums = [3,2,1]

Output:

  (int[]) [1,2,3]

Solution

C C++ Golang Java Python

void nextPermutation(int* nums, int numsSize){
    int i = numsSize - 2;
    while(i>=0 && nums[i] >= nums[i+1]) {
        i--;
    }
    if (i >= 0) {
        int j = numsSize - 1;
        while(nums[j] <= nums[i]) {
            j--;
        }
        swap(nums, i, j);
    }
    reverse(nums, numsSize, i+1);
}

void swap(int* nums, int i, int j) {
    int temp = nums[i];
    nums[i] = nums[j];
    nums[j] = temp;
}

void reverse(int* nums, int numsSize, int start) {
        int i = start, j = numsSize - 1;
        while(i < j) {
            swap(nums, i, j);
            i++;
            j--;
        }
    }

class Solution {
public:
    void nextPermutation(vector<int>& nums) {
        int n = nums.size();
        int i = n - 2;
        while(i >= 0 && nums[i] >= nums[i+1]) {
            i--;
        }
        if (i >= 0) {
            int j = n - 1;
            while(nums[j] <= nums[i]) {
                j--;
            }
            swap(nums, i, j);
        }
        reverse(nums, i+1);
    }

    void swap(vector<int>& nums, int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }

    void reverse(vector<int>& nums, int start) {
        int i = start, j = nums.size() - 1;
        while(i < j) {
            swap(nums, i, j);
            i++;
            j--;
        }
    }
};

package next_permutation

func nextPermutation(nums []int)  {
	i := len(nums) - 2
	for i>=0 && nums[i+1] <= nums[i] {
		i--
	}
	if i>=0 {
		j := len(nums) - 1
		for nums[j] <= nums[i] {
			j--
		}
		swap(nums, i, j)
	}
	reverse(nums, i+1)
}

func swap(nums [] int, x int, y int) {
	temp := nums[x]
	nums[x] = nums[y]
	nums[y] = temp
}

func reverse(nums []int, start int) {
	left, right := start, len(nums) - 1
	for left < right {
		swap(nums, left, right)
		left++
		right--
	}
}

public class Solution {
    public void nextPermutation(int[] nums) {
        int i = nums.length - 2;
        while (i >= 0 && nums[i + 1] <= nums[i]) {
            i--;
        }
        if (i >= 0) {
            int j = nums.length - 1;
            while (nums[j] <= nums[i]) {
                j--;
            }
            swap(nums, i, j);
        }
        reverse(nums, i + 1);
    }

    private void reverse(int[] nums, int start) {
        int i = start, j = nums.length - 1;
        while (i < j) {
            swap(nums, i, j);
            i++;
            j--;
        }
    }

    private void swap(int[] nums, int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }js
}

from typing import List


class Solution:
    def nextPermutation(self, arr: List[int]) -> None:
        """
        Do not return anything, modify nums in-place instead.
        """
        n = len(arr)
        i, j = n - 2, 0
        while i >= 0 and arr[i] >= arr[i + 1]:
            i -= 1
        j = i + 1
        if i >= 0:
            j = n - 1
            while j >= 0 and arr[j] <= arr[i]:
                j -= 1
            arr[i], arr[j] = arr[j], arr[i]
        start, end = i + 1, n - 1
        while start < end:
            arr[start], arr[end] = arr[end], arr[start]
            start += 1
            end -= 1