There are n cities connected by some number of flights. You are given an array flights where flights[i] = [from, to, price] indicates that there is a flight from city fromi to city toi with cost pricei.

You are also given three integers src, dst, and k, return the cheapest price from src to dst with at most k stops. If there is no such route, return -1.

Test Cases

Example 1:

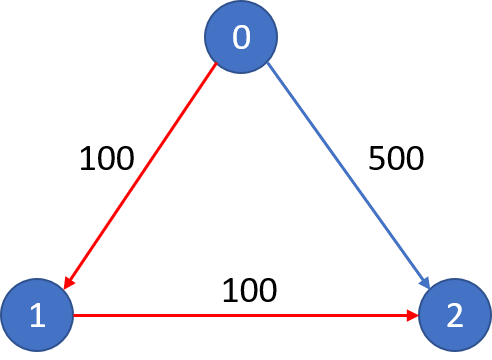
Cheapest flight

Input: n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 1
Output: 200
Explanation: The graph is shown.
The cheapest price from city 0 to city 2 with at most 1 stop costs 200, as marked red in the picture.

Example 2:

Cheapest flight

Input: n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 0
Output: 500
Explanation: The graph is shown.
The cheapest price from city 0 to city 2 with at most 0 stop costs 500, as marked blue in the picture.

Solution

class Solution {
    public int findCheapestPrice(int n, int[][] flights, int src, int dst, int k) {
        int graph[][] = new int[n][n];
        for (int i = 0; i < flights.length; i++) {
            graph[flights[i][0]][flights[i][1]] = flights[i][2];
        }
        int ans = findCheapestPrice(src, dst, graph, k + 1, new int[n + 1][n + 1][k + 2]);
        return ans >= 1000000 ? -1 : ans;
    }

    int findCheapestPrice(int src, int dst, int graph[][], int k, int dp[][][]) {
        if (dst == src) {
            return 0;
        }
        if (k == 0) {
            return 1000000;
        }
        if (dp[src][dst][k] != 0) {
            return dp[src][dst][k];
        }
        int min = 1000000;
        for (int i = 0; i < graph[src].length; i++) {
            if (graph[src][i] != 0) {
                min = Math.min(min, graph[src][i] + findCheapestPrice(i, dst, graph, k - 1, dp));
            }
        }
        return dp[src][dst][k] = min;
    }
}
Time Complexity: O(nk)
Space Complexity: O(n2k)