Given a string s, partition s such that every substring of the partition is a palindrome. Return all possible palindrome partitioning of s.

A palindrome string is a string that reads the same backward as forward.

How to Solve

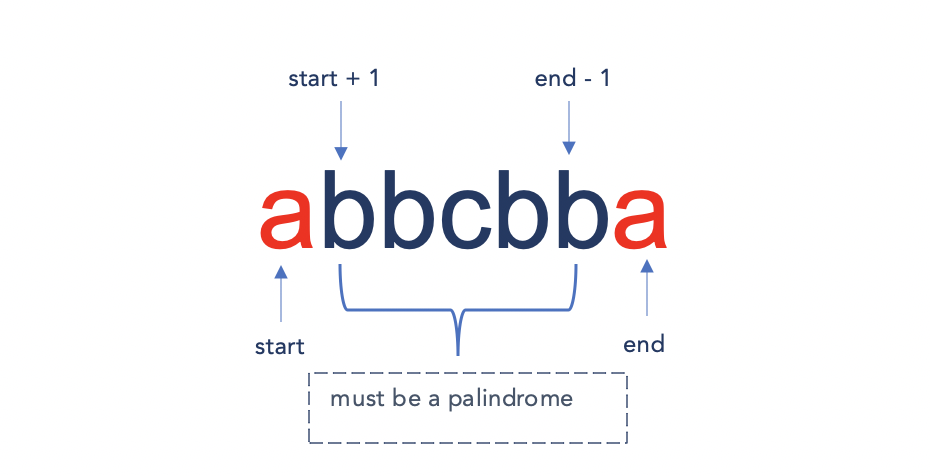
A given string s starting at index start and ending at index end is a palindrome if following conditions are satisfied :

  1. The characters at start and end indexes are equal.
  2. The substring starting at index start+1 and ending at index end−1 is a palindrome.

Palindrome

Let N be the length of the string. To determine if a substring starting at index start and ending at index end is a palindrome or not, we use a 2 Dimensional array dp of size NxN where,

dp[start][end]=true , if the substring beginning at index start and ending at index end is a palindrome.

Otherwise, dp[start][end] ==false.

Also, we must update the dp array, if we find that the current string is a palindrome.

Test Cases

Example 1:

Input: s = "aab"
Output: [["a","a","b"],["aa","b"]]

Example 2:

Input: s = "a"
Output: [["a"]]

Solution

class Solution {
public:
    vector<vector<string>> partition(string s) {
        int n = s.length();
        vector<vector<string>> result;
        vector<vector<bool>> dp(n, vector<bool>(n, false));
        vector<string> current;
        backtrack(s, dp, 0, current, result);
        return result;
    }

    void backtrack(string s, vector<vector<bool>> &dp, int start, vector<string> &current, vector<vector<string>> &result) {
        if (start >= s.length()) {
            result.push_back(current);
            return;
        }
        for(int pos=start; pos<s.length(); pos++) {
            if (s[start] == s[pos] && (pos - start <= 2 || dp[start+1][pos-1])) {
                dp[start][pos] = true;
                current.push_back(s.substr(start, pos+1-start));
                backtrack(s, dp, pos+1, current, result);
                current.pop_back();
            }
        }
    }
};
class Solution {
    public List<List<String>> partition(String s) {
        int len = s.length();
        boolean[][] dp = new boolean[len][len];
        List<List<String>> result = new ArrayList<>();
        backtrack(result, s, 0, new ArrayList<>(), dp);
        return result;
    }

    void backtrack(List<List<String>> result, String s, int start, List<String> currentList, boolean[][] dp) {
        if (start >= s.length()) result.add(new ArrayList<>(currentList));
        for (int end = start; end < s.length(); end++) {
            if (s.charAt(start) == s.charAt(end) && (end - start <= 2 || dp[start + 1][end - 1])) {
                dp[start][end] = true;
                currentList.add(s.substring(start, end + 1));
                backtrack(result, s, end + 1, currentList, dp);
                currentList.remove(currentList.size() - 1);
            }
        }
    }
}
from typing import List


class Solution:
    def partition(self, s: str) -> List[List[str]]:
        n = len(s)
        dp = [[False for _ in range(n)] for _ in range(n)]
        res = []
        self.backtrack(s, 0, dp, [], res)
        return res

    def backtrack(self, s, start, dp, current, res):
        if start >= len(s):
            res.append(list(current))
            return
        for end in range(start, len(s)):
            if s[start] == s[end] and (end-start <= 2 or dp[start+1][end-1]):
                dp[start][end] = True;
                current.append(s[start:end+1])
                self.backtrack(s, end+1, dp, current, res)
                current.pop()
Time Complexity: O(n2n)
Space Complexity: O(n2)