Given a binary tree and target node. By giving the fire to the target node and fire starts to spread in a complete tree. The task is to print the total time to burn every node of the binary tree
Rules for burning the nodes :
- Fire will spread constantly to the connected nodes only.
- Every node takes the same time to burn.
- A node burns only once.
Test Cases
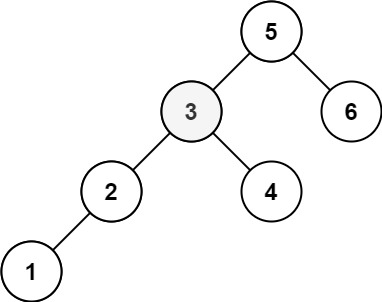
Input:
(TreeNode) root = [5,3,6,2,4,null,null,1]
(int) target = 4
Output:
(int) 4
Explanation
Step 1: burn 4
Step 2: burn 3
Step 3: burn 2, 5
Step 4: burn 1, 6
Input:
(TreeNode) root = [5,3,6,2,4,null,null,1]
(int) target = 3
Output:
(int) 3
Explanation
Step 1: burn 3
Step 2: burn 2,4,5
Step 3: burn 1, 6
Solution
class TreeNode{
int data;
TreeNode left;
TreeNode right;
}
class BurningTree{
public int minTimeToBurnTree(TreeNode root,int target){
Map<TreeNode, TreeNode> parentMap=new HashMap<>();
Queue<TreeNode> queue=new LinkedList<>();
Set<TreeNode> visited=new HashSet<>();
queue.offer(root);
TreeNode targetNode=null;
int steps=0;
while(!queue.isEmpty()){
TreeNode node=queue.poll();
if (node.data==target){
targetNode=node;
}
if(node.left!=null){
queue.offer(node.left);
parentMap.put(node.left,node);
}
if(node.right!=null){
queue.offer(node.right);
parentMap.put(node.right,node);
}
}
if(targetNode==null){
return -1;
}
queue.clear();
queue.offer(targetNode);
visited.add(targetNode);
while(!queue.isEmpty()){
int size = queue.size();
for(int i=0; i<size; i++){
TreeNode node=queue.poll();
TreeNode parent=parentMap.get(node);
if(node.left!=null && !visited.contains(node.left)){
queue.offer(node.left);
visited.add(node.left);
}
if(node.right!=null && !visited.contains(node.right)){
queue.offer(node.right);
visited.add(node.right);
}
if(parent!=null && !visited.contains(parent)){
queue.offer(parent);
visited.add(parent);
}
}
if(!q.isEmpty()) steps++;
}
return steps;
}
}